Language Model (2) Smoothing

Language Model Series Post

Smoothing

Language Model은 Train set의 통계에 기반하여 만들어지는 것이기 때문에 Train set이 언어의 모든 경우를 포함하는 경우(사실상 불가능)를 제외하고는 Co-occurrence matrix 중간 중간에 count가 0인 값들이 존재하게 된다. 이렇게 Count가 0인 항목들에 대해서는 확률이 0으로 나오는 zero probability 문제가 발생하여 Language Model을 범용적으로 사용하기 힘들게 만든다. 이러한 문제점들을 해결하기 위해 사용된 Smoothing의 개념은 간단히 말해서 Train set에서 한번도 나오지 않은 Co-occurrence matrix값들에 대해 0이 아니라 특정값을 추가하여 확률이 Vocab안에 있는 쌍에 대해서는 절대 확률이 0이 나오지 않도록 완화하는 것이다. Smoothing을 어떻게 하느냐에 따라서 크게 다음과 같이 3개로 나눌 수 있다.

Laplace smoothing
1. Add one smoothing
2. Add-K smoothing
Back off and interpolation
Kneser-Ney smoothing

Laplace smoothing (Additive smoothing)

Laplace smoothing은 Smoothing 중 가장 간단한 개념으로 상수를 더해주어 Zero count를 없애서 zero probability 문제를 해결하고자 한 방법이다. 어떤 상수를 더하느냐에 따라 그 모델이 달라지게 된다.

Add-one smoothing

Add-one smoothing은 생각해볼 수 있는 가장 간단한 Laplace Smoothing으로 N-gram의 모든 count에 대해 1을 더해주는 것이다. 방법이 간단하기 때문에 구현하기도 쉽지만 그만큼 성능이 잘 나오지는 않아 최근 잘 사용하지는 않는다. 하지만, Text classification과 같은 비교적 간단한 task에 대해서는 아직까지도 잘 쓰인다고 한다. 그리고 가장 기초적인 Smoothing method이기 때문에 다른 method들의 Baseline 역활을 한다. Unigram에 Add-one smoothing 을 적용한 예시를 들어보면 다음과 같다.

$\text{Original:}\quad P(w_i)=\frac{C_i}{N}$ $\eqalign{ \text{Add-one:}\quad P(w_i) &=\frac{C_i + 1}{N + V} \\ &=\frac{C_i^*}{N} }$ $C_i : \text{Count of i-th word}, N = \Sigma_i C_i\\ V: \text{Number of vocab}, C_i^* = \frac{C_i+1}{C_i}\frac{N}{N+V}$

위에서 새로운 Count로 바꾼 것은 Add-one smoothing이 적용되었을 때 기존의 Count와 보다 쉽게 비교하기 위함이다. 결과적으로 기존의 Zero였던 값들을 제외하고 나머지의 값들은 전체적으로 Count가 감소하게 된다. 보다 Count가 많을수록 많이 상대적으로 감소하게 되는데 이러한 측면때문에 Smoothing method를 기존의 Count를 깍아서 zero count에 나눠준다는 의미로 discount method라고도 한다. 어느정도 Discount가 되었는지는 다음 discount ratio를 통해 구할 수 있다.

$d_c = \frac{C^*}{C}$

Unigram이외에도 Bigram, Trigram 이상에 대해서도 위와 같이 각각에 대해 Count를 1씩 더해주고 이를 Normalize하는 방식으로 Add-one smoothing을 적용하면 된다.

Add-k smoothing

Add-one smoothing이 전체 Statistics에 1씩 더해주었다면 Add-k smoothing은 이름에서 짐작할 수 있다시피 전체 Statistics에 k만큼 더해주는 방법이다. 1대신에 조금 더 나은 결과를 얻기 위해 0.2, 0.5등 여러 k 값을 사용하며 여러 시도를 하는 것으로 생각할 수 있는데, train set에 대한 적절한 k값은 dev set을 통해 찾을 수 있을지라도 여전히 제대로 작동하지는 않는다. Add-k smoothing의 확률 함수는 다음과 같이 구할 수 있다.

$P^*_{add-k}(w_n|w_{n-1}) = \frac{C(w_{n-1}, w_n) + k}{C(w_{n-1}) + kV}$

back off and interpolation

하나의 Language Model(Unigram, Bigram 등…)의 성능을 향상시키기 위해 Statistics에 상수를 추가하던 Add-k smoothing과는 달리 back off and interpolation은 여러 Language Model을 함께 사용하여 보다 나은 성능을 얻으려는 방법이다. 여러 Model을 사용한다는 점에서 back off, interpolation method는 공통점을 가지고 있지만 어떻게 적용한지에 따라서 차이가 존재한다.

back off

back off를 사전에 검색하면 “뒤로 물러나다”라는 뜻임을 알 수 있는데 language model에서 back off는 그 뜻 그대로 적용된다. 예를 들어, 하나의 Train set으로부터 Unigram, bigram, trigram을 만들었다고 생각해보자. 보통은 trigram이 보다 우수하기 때문에 trigram을 사용하기 마련이다. 하지만, 그만큼 statistics가 부족해 zero-probability 문제가 발생할 수 있는데 그러한 상황에는 trigram이 아니라 bigram의 결과를 사용하는 것이다. 즉, Higher-order (Higher n gram)에서 zero count라면 n-1 gram의 값을 사용하며 이를 Recursive로 사용하게 된다. 기본적인 back off algorithm은 다음 식을 통해 표현할 수 있다.

$P_{BO}(w_n|w_{n-N+1}, \cdots, w_{n-1}) = \cases{ P(w_n|w_{n-N+1}, \cdots, w_{n-1}) & \text{if} c_{n-1}, \cdots, c_n >0 \cr P_{BO}(w_n|w_{n-N+2}, \cdots, w_{n-1}) }$

하지만 이대로 사용하면 큰 문제가 있는데, Order가 다른 N-gram을 같이 사용하면 전체 확률의 합이 1을 넘어갈 수도 있게 된다. 이러한 문제는 각 N-gram에 대한 statistics가 다르기 때문에 이를 해결하기 위해서는 앞에서 Smoothing에서 나온 discount개념이 필요하다. 각각에 대해 적절한 값을 곱해주어 보정해주면 된든데 먼저, Back off을 적용할 때 count가 있어서 바로 확률값을 사용할 수 있는 경우에는 discounting된 확률을 사용한다. 그리고 count가 0이어서 한단계 낮은 N-gram에 대해 recursive하게 진행되는 경우에는 distributing function $\alpha$ 를 곱해준다. 이렇게 back off에 smoothing이 적용된 걸 Katz back off라고 한다. Katz back off를 적용한 확률은 다음과 같다.

$P_{BO}(w_n|w_{n-N+1}, \cdots, w_{n-1}) = \cases{ P^*(w_n|w_{n-N+1}, \cdots, w_{n-1}) & \text{if} c_{n-1}, \cdots, c_n >0 \cr \alpha(w_{n-N+1}, \cdots, w_{n-1})P_{BO}(w_n|w_{n-N+2}, \cdots, w_{n-1}) }$

Katz backoff는 보통 Good Turing이라 불리는 방법과도 같이 사용되는데 Good-Turing backoff 방법은 Good-Turing smoothing, $P^*$ 와 $\alpha$ 를 계산하는 과정이 수반된다.

Interpolation

앞에서의 Backoff가 Count가 0인 경우 Lower order n gram의 결과를 Recursive하게 사용하는 방법이었다면 Interpolation은 여러 order n gram 값을 linear combination하여 한번에 사용한다. Unigram부터 Trigram까지의 model을 interpolation하는 경우의 확률은 다음과 같다.

$\begin{align} P_{simple}(w_n|w_{n-2}, w_{n-1}) &= \lambda_1P(w_n|w_{n-2},w_{n-1}) &\text{Trigram} \cr &= \lambda_2P(w_n|w_{n-1}) &\text{Bigram} \cr &= \lambda_3P(w_n) &\text{Unigram} \end{align}$ $(\Sigma_i (\lambda_i) = 1)$

여기서 각 n gram값의 $\lambda$ 는 dev set과 같이 train set과 구별된 held-out corpus로부터 적절한 값을 찾아내면 된다. 위의 Interpolation에서 기본적으로 $\lambda$ 는 단순한 상수이지만 이 $\lambda$ 를 단어의 함수로 만들어 Context정보를 적용할 수도 있다. Context가 적용된 Interpolation 확률은 다음과 같다.

$\begin{align} P_{context}(w_n|w_{n-2}, w_{n-1}) &= \lambda_1(w_{n-2}, w_{n-1}) P(w_n|w_{n-2},w_{n-1}) &\text{Trigram} \cr &= \lambda_2(w_{n-2}, w_{n-1}) P(w_n|w_{n-1}) &\text{Bigram} \cr &= \lambda_3(w_{n-2}, w_{n-1}) P(w_n) &\text{Unigram} \end{align}$

Kneser-Ney smoothing

Absolute Discounting

마지막 순서답게 이 Smoothing은 가장 잘 작동하는 smoothing으로 absolute discouning에 뿌리를 두고 있다. absolute discounting은 Train set과 test set(heldout set) 각각에 대한 bigram의 count를 비교한 Church와 Gale의 실험으로부터 제시되었다. 해당 실험에서는 Train set과 test set으로 각각 2200만개의 단어를 사용하였는데, 아래 표에서 볼 수 있듯이 신기하게도 train set에서 0, 1번씩 등장한 bigram을 제외하고 나머지 2번 이상 등장한 bigram 쌍들은 평균적으로 test set에서 약 0.75정도번 정도 적은만큼 등장하였다.

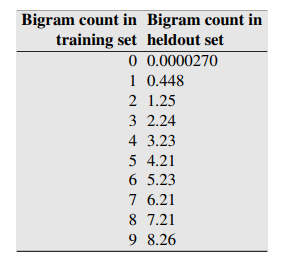
이 실험 결과를 보고 쉽게 생각할 수 있는 것은 전체 통계에 0.75처럼 특정한 값을 빼주는 것이다. Absolute discounting은 이 아이디어에 기반한 것으로 수정된 특정한 상수를 빼는 Bigram 확률에 unigram을 interpolation한 확률은 다음과 같다.

$P_{absolute discounting}(w_i|w_{i-1})=\frac{C(w_{i-1}w_i) - d}{\Sigma_vC(w_{i-1}v)} + \lambda(w_{i-1}P_{w_i})$

먼저 앞의 항은 discounted bigram으로 기존의 bigram 식을 구하는 확률의 분모에 d를 빼는 것을 확인할 수 있다. 여기서의 d는 0.75로 고정해서 사용하거나 보통 0.5를 사용하고 count가 1인 bigram에 대해서만 1로 적용할 수도 있다.

Kneser-Ney discounting

Absolute discounting의 수정된 버전인 Kneser-Ney discounting에서는 Continuation이라는 새로운 개념이 등장한다. Continuation에 대해 알기 위해 다음과 같은 문장를 살펴보자.

$\text{I can't see without my reading ___}$

glasses와 같은 단어가 적합해보이지만 만약 Unigram에서 Hong Kong이라는 단어가 많이 나와 Kong이 빈도수가 가장 높다면 Kong이 나오게 될 것이다. Unigram에서는 Context에 대한 정보를 담을 수가 없기 때문인데 이 점을 해결하기 위해서 Continuation이 사용되었다. Continuation은 단순히 단어의 빈도수를 보는 것이 아니라 다른 단어와 얼마나 함께 사용되었는지에 주목한다. 이를 적용하기 위해서 Continuation에서는 구하고자 하는 단어가 Bigram의 2번째 단어로 얼마나 사용되었는지 계산하고 전체 Bigram count로 나누어주어 확률을 계산한다.

$P_{CONTINUATION}(w) = \frac{|\{v:C(vw)>0\}|}{|\{(u', v'):C(u'w')>0)\}|}$

앞의 예제에서 다룬 Kong에 대한 Continuation확률은 다음과 같이 구할 수 있다.

Kong이 두번째 단어로 나오는 Bigram count를 더한다. (만약, Train set에서 Kong이 Hong Kong에서 6번, King Kong에서 2번나왔다면 전체 Count는 6+2=8이 된다.)
Bigram의 전체 Count를 더한다.
1번에서 구한 Kong의 Continuation Count를 2번에서 구한 값으로 나누면 Kong의 Continuation 확률이 된다.

Kneser Ney smoothing은 기본적인 Absolute discounting에 Unigram 대신에 continuation 개념을 적용한 것으로 다음과 같이 얻을 수 있다.

$P_{KN}(w_i|w_{i-1}) = \frac{max(c_{KN}(w_{i-1}w_i) -d,0)}{C(w_{i-1}) + \lambda(w_{i-1})P_{CONTINUATION}(w_i)}$ $\lambda(w_{i-1}) = \frac{d}{\Sigma_vC(w_{i-1}v)}|\{w:C(w_{i-1}w)>0\}|$

$\lambda$ 는 continuation을 적용하기 위한 normalizing constant로서 discount ratio와 continuation 가중치가 곱해진 것으로 볼 수 있다. 앞에서의 Kneser Ney smoothing은 Bigram에 대한 것으로 일반적인 n gram에 대해서는 다음의 식을 통해 얻을 수 있다.

$P_{KN}(w_i|w_{n+1}^{i-1}) = \frac{max(c_{KN}(w_{n+1}^{i}) -d,0)}{\Sigma_v c_{KN}((w_{n+1}^{i-1}v))} + \lambda(w_{n+1}^{i-1})P_{KN}(w_i|w_{n+2}^{i})$

Back off를 통해 Recursive하게 구한 값을 Interpolation을 통해 더하는 형태인데 핵심은 $c_{KN}$ 에 있다. 이 값은 Highest order n gram(Unigram, Bigram, Trigram을 쓴 경우 Trigram)의 경우 count 그대로 적용하고 나머지 n gram들에 대해서는 continuation count를 적용한다. Kneser Ney 확률을 Recursive하게 계속 구하면 마지막 Unigram에 도착할텐데, Unigram의 확률은 absolute discounting에 uniform distribution을 적용하여 다음과 같다.

$P_{KN}(w)=\frac{max(c_{KN}-d,0)}{\Sigma_{w'}c_{KN}(w')} + \lambda(\epsilon)\frac{1}{V}$

$\lambda(\epsilon)$ 은 Empty string or unknown word 에 대한 것으로 만약 Vocab에 없는 단어가 나타나면 이에 대한 확률은 $$\frac{\lambda(\epsilon)}{V}$$이 되며 $$\lambda(\epsilon)$$를 조정하여 그 비율을 조정할 수 있다.

Kneser-Ney smoothing 중 가장 성능이 우스수한 버전은 Chen과 Goodman (1998)이 만든 modified Kneser-Ney smoothing으로 discount (d)를 하나만 쓰는 것이 아니라 여러 개를 쓰는 것이다.

여기까지 Language model에서 등장하는 zero probability 문제 해결과 성능 향상을 위해 사용된 Smoothing의 여러 방법들에 대해 살펴보았다. 다음 Language model 마지막 Post에서는 이전 Post에서 다루었던 Perplexity의 entropy와의 관계를 Informatics 관점에서 살펴보겠다.

출처

Stanford Speech and Language Processing