We may want to ask when we want to deal with important area of posterior interval or what is a interval that contains 95% of posterior probability in some meaningful way. This would be equivalent to a frequent confident interval in a concept. There are two famous way. One is equal tailed interval and another is HPD(Highest posterior density)
Equal tailed interval
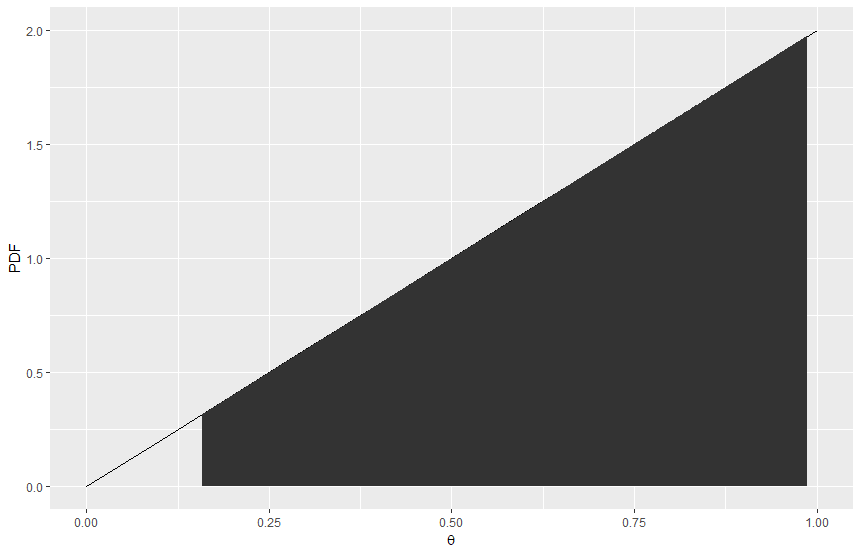
We put equal amount of probability in each tail. To make 95% interval, we'll put .025 in each tail. To calculate that point, we need to know quantile which can be calculated by hand or other program like R. We will use the posterior distribution of parameter which is start from unifrom distribtuion and observing one head. Following equation is the process of calculating quantile and 95% interval
$$P(\theta \le q|Y=1) = \int^q_0 2\theta d\theta = q^2$$
$$P(\sqrt{.025} \le \theta \le \sqrt{.975}) = P(.158 \le \theta \le .987) = .95$$
We can say under posterior, there's 95% probability that theta is in this interval. Also, we can see this kind of plot.
HPD(Highest Posterior Density)
In this concept, The important region is including the highest posterior density. For example, the highest posterior density area is right side of the previous plot.
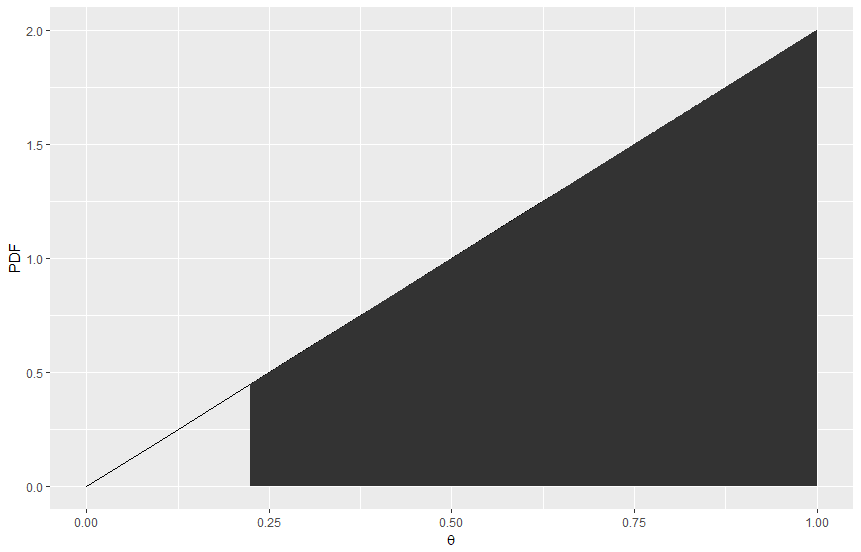
In summary, the posterior distribution describes our understanding of our uncertainty combinated from our prior perspective and the actual data. With a probability density function, we can make intervals and talk about probability of data being at the interval. This is better appoach than the frequentist paradigm which can only get confident interval cannot tell the probability of whether the theta is in the region or not.
Frequentist confidence interval have the interpolation that if you were to repeat many times the process of collecting data and computing a 95% confidence interval, then on the average that 95% of those interval's would contain the true parameter value However, once you observe data and compute an interval the true value is either in the interval or it is not, but you can't tell with the Frequentist paradigm.
Bayesian credible intervals have the interpolation that your posterior probability that the parameter is in credible interval is 95%