Let's deal with bayesian theorem more detail. In the equation, It is often hard to calculate integral of denominator. Actually, the denominator is the meaning of normalizing const. So, the important part is numerator side. $$f(\theta|y)=\frac{f(y|\theta)f(\theta)}{f(y)}=\frac{f(y|\theta)f(\theta)}{\int f(y|\theta) f(\theta)}$$ $$f(\theta|y)=\frac{likelihood\cdot prior}{normalizing const} \varpropto likelihood\cdot prior$$
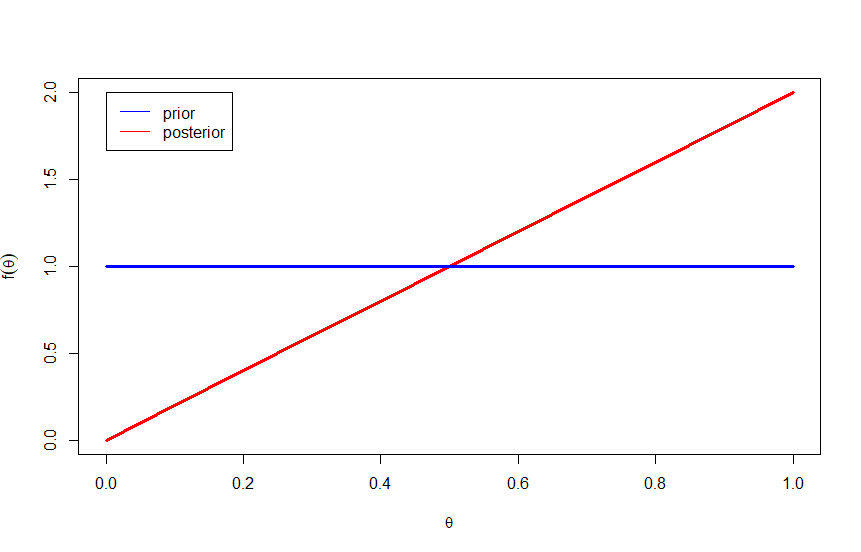
Suppose we are looking at the coin and it has unkown probability theta of coming up heads. Also suppose we express ignorance about the value of theta by assigning it a uniform distribution. We can update our prior with data if there are one head event in one flip like this. $$\theta \sim U[0,1]$$ $$f(\theta)=I_{0\le\theta\le1}$$ $$f(\theta|Y=1)=\frac{f(y=1|\theta)f(\theta)}{f(y)}=\frac{\theta^1(1-\theta)^{1-1}I_{0\le\theta\le1}}{\int_{-\infty}^\infty\theta^1(1-\theta)^{1-1}I_{0\le\theta\le1}d\theta}$$ $$=\frac{\theta I_{0\le\theta\le1}}{\int_0^1\theta d\theta}=2\theta I_{0\le\theta\le1}$$ $$f(\theta|y)\varpropto f(y|\theta)\cdot f(\theta) = \theta I_{0\le\theta\le1}$$
We can also plot the prior distribution and posterior distribution after one event. There are changes due to one head observation.