Boyer-Moore string search algorithm

Posted by JongHyun on October 3, 2018

주어진 Text에서 특정 Pattern 문자열이 있는지 없는지를 알기 위해서는 어떻게 해야할까? 가장 간단한 방법은 Text의 처음부터 마지막까지 일일히 비교하는 것이다. 이는 가능한 한 모든 경우를 확인하는 것이기에 Brute-force method라고도 불린다. Brute-force method는 직관적이고 구현하기도 쉽지만 효율적인 방법이라고는 할 수 없다. 특정 문자열이 속해있는지를 확인하는 알고리즘은 여러 가지가 있지만 이번 Post에서는 대표적인 Boyer-Moore string-search algorithm을 확인해볼 것이다.

Boyer-Moore string-search algorithm

Boyer-Moore algorithm와 Brute-force method의 첫번째 차이점은 바로 Text string(이하 T)와 Pattern string(이하 P)를 비교하는 것이 아니라 P를 분석하는 전처리과정(Preprocess)을 거친다는 점이다. 전처리과정에서 얻어진 결과물은 T와 P의 비교불일치가 일어났을 때, Brute-force method처럼 비교 위치를 무조건 한 칸만 이동시키는 것이 아니라 문자의 배열에 따라 최소 한 칸부터 최대 P의 길이만큼 이동시킨다. 이는 비약적으로 비교 속도를 향상시키며 미리 분석한 정보를 사용하기에 P가 T에 비해 짧을 수록, T가 길수록 더욱더 상대적인 효율이 향상된다.

두번째 차이점은 T의 비교하고자 하는 sub-string과 P를 비교할 때에 앞의 문자부터 비교하는 것이 아니라 뒤의 문자부터 비교한다는 점이다. 이는 두 문자열을 비교시에 앞의 문자가 일치하더라도 뒤의 문자가 불일치하면 비교할 필요가 없음을 생각하면 쉽게 타당성을 납득할 수 있다. 뒤에서부터 검사하는 방식은 P의 shift를 효과적으로 수행할 수 있도록 만들어준다. 이러한 차이점을 가지고 있는 Boyer-Moore algorithm의 순서를 간단히 정리해보면 다음과 같다.

  1. Pattern P와 Text T는 같은 시작점에 정렬된다.
  2. P[m-1]와 T[m-1]를 비교하며 일치시에 앞의 character를 비교해 나간다. (m : T의 길이)
  3. 비교는 P의 Beginning까지 진행되거나 비교 불일치가 일어날 때까지 진행한다.
  4. 불일치가 일어났을 경우에는 P의 전처리 정보를 활용해 가능한 한 최대의 Shift를 반영한다.
    ex) 만약 shift = 3이라면 P[3 + m- 1] 와 T[m-1]에서부터 비교 시작.
  5. 비교는 새로운 Alignment에서 진행된다.
  6. 위의 과정을 반복한다

Shift rules

Bad character rule

Bad character rule은 비교가 실패한 T의 character를 이용하는 rule이다. 예를 들어, T와 P를 비교하던 중 T[i], P[j]에서 불일치가 일어났다고 가정해보자. 이 경우, Bad character rule의 적용은 크게 3가지 경우로 나뉘게 된다.

  1. T[i]와 같은 문자가 아직 비교하지 않은 P에 존재하는 경우(T[i] == P[k] (k < j)) 
→ T의 비교 시작위치를 `j - k`만큼 shift 시킨다.
  1. T[i]와 같은 문자가 이미 비교한 P에 존재하는 경우(T[i] == P[k] (k > j))
→ T의 비교 시작위치를 한칸 shift 시킨다.
  1. T[i]와 같은 문자가 아직 비교하지 않은 P에 존재하지 않는 경우
→ T의 비교 시작위치를 `j + 1`만큼 shift 시킨다.

다음 그림을 보면 보다 쉽게 이해할 수 있다.

algorithm sample Bad character rule example

Rule을 적용하기 위해서 가장 먼저 해야 할 것은 모든 Alphabet들 각각에 대해서 P 내에서의 위치를 저장하는 array를 만드는 전처리과정을 거치는 것이다. P에 존재하지 않는 문자들에 대해서는 P의 길이를 저장하며 중복되는 문자들에 대해서는 가장 오른쪽에 있는 문자의 위치 정보만을 저장한다.

구현

아래의 코드는 Bad character rule을 사용하기 위해서 P의 character 위치 정보를 담아두는 전처리 과정을 구현한 것이다. 여기서 만들어진 delta[] array를 이용해서 shift를 적용할 수 있게 된다.

#define ALPH_LEN 256 // Alphabet뿐만 아니라 전체 character를 다루기 위해
void makeDelta(int delta[], char pat[], int patLen){
    for(int i=0;i<ALPH_LEN;++i){
        delta[i] = patLen; // pattern의 길이로 초기화
    }
    for(int i=0;i<patLen;++i){
        delta[pat[i]] = (patLen - 1 - i); // Last index에서부터의 길이를 저장
    }
}

전처리과정에서 구한 delta[]를 적용하는 전체 코드는 다음과 같다. 기본적인 규칙은 위에서 말한대로 delta[]에 담겨있는 P의 문자 위치 정보를 이용해서 shift를 시키는 것이며 만약 해당 character가 이미 비교되었다면 한 칸만 이동한다.

void search(char *text, char *pat){

    int textLen = mstrlen(text);
    int patLen = mstrlen(pat);

    // Make delta function which will be used for bad-character shift
    makeDelta(delta, pat, patLen);

    // Pattern과 같은 길이의 Substring의 끝에서 비교 시작
    int i = patLen - 1; 
    while (i < textLen) {
        int j = patLen - 1; // 항상 Pattern의 끝에서부터 비교
        while (j >= 0 && text[i] == pat[j]) {
            --j;
            --i;
        }
        if (j < 0) {
            printf("Pattern found at %d\n", i + 1);
            i += patLen + 1; // 이전 비교 시작점에서 한 칸 앞으로 이동
            continue;
        }
        
        int shift, checkedLength = patLen - 1 - j;
        if (checkedLength > delta[text[i]])
            shift = checkedLength + 1; // 이전 시작점에서 한 칸 앞으로 이동
        else 
            shift = delta[text[i]]; 

        i += shift;
    }
}

구현 코드에서 볼 수 있듯이, Bad character rule은 굉장히 이해하기 쉬우며 구현하기도 쉽다. 하지만, 항상 최고의 효율을 보여준다고 할 수는 없다. 예를 들어, Pattern 내에 여러개의 중복된 문자가 존재할 경우에 한 칸씩만 앞으로 이동하는 경우가 생길 수 있다. 이는 전처리과정에서는 character 들 중 가장 오른쪽의 위치 정보만 저장하기 때문이다. Bad character rule의 비효율문제를 해결하기 위해서 보통 Boyer-Moore algorithm은 Bad character rule만을 사용하는 것이 아니라 Good suffix rule이라는 다른 규칙을 함께 사용한다.

Good suffix rule

Bad character rule과는 다르게 Good suffix rule은 이름에서 알 수 있는 것처럼 이미 비교 과정에서 일치한 문자들(일치한 T의 sub-string을 t라 하자)의 정보를 이용한다. Good suffix rule은 크게 3가지의 경우로 나눌 수 있다.

  1. P에서 이미 비교한 부분을 제외하고 t와 동일한 string이 존재하는 경우
  2. P의 prefix와 t의 suffix들 중 일치하는 string이 존재하는 경우
  3. P에 t와 일치하는 string이 없는 경우

Case 1. t와 동일한 string이 P에 존재하는 경우

Case 1은 이미 검사한 t와 일치하는 string이 P 내부에 여러 개 존재할 수 있음을 이용하는 것이다. 이를 적용하는 방법은 간단한데, T와 P의 불일치가 일어난 경우 이미 확인된 t와 일치하는 string을 P에서 찾고 만약 있다면 해당 index 차이만큼 shift시키는 것이다. 아래 그림을 보면 보다 명확하게 이해할 수 있다. 하지만, 이 방식은 Boyer-Moore의 weak rule case로 생각보다 효율적이지 않다. 보다 뒤에서 이를 개량한 strong rule을 다뤄보겠다.

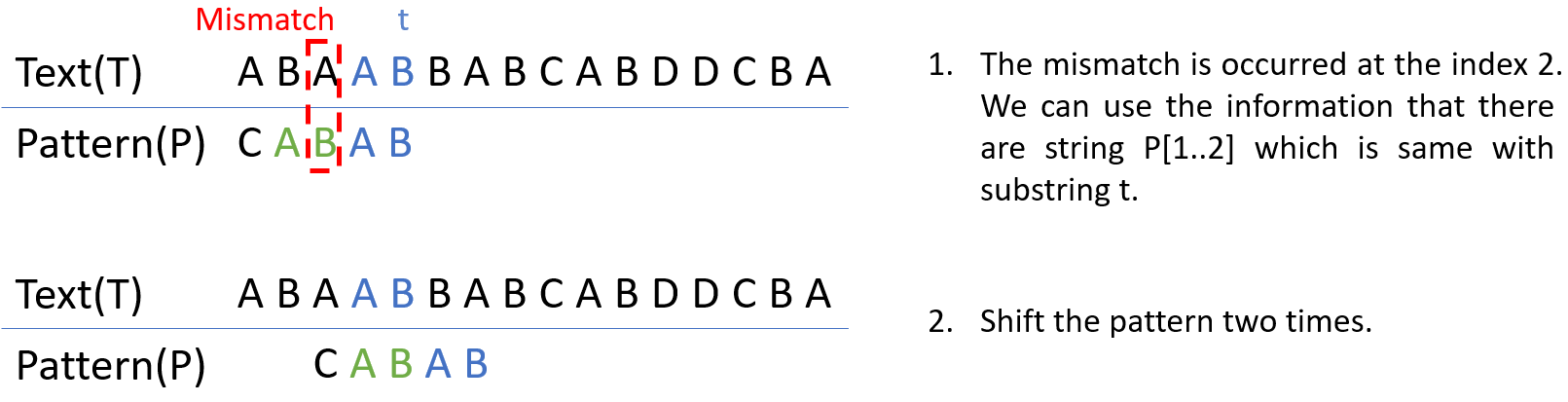
good_suffix_case_1 Good suffix rule case 1 example

Case 2. P의 prefix와 t의 suffix가 일치하는 경우

Case 2는 Case 1처럼 정확히 일치하는 string을 찾는 것이 아니라 P의 prefix와 일치하는 t의 suffix를 찾고 불일치가 일어났을 때 해당 index로 shift하는 것이다.

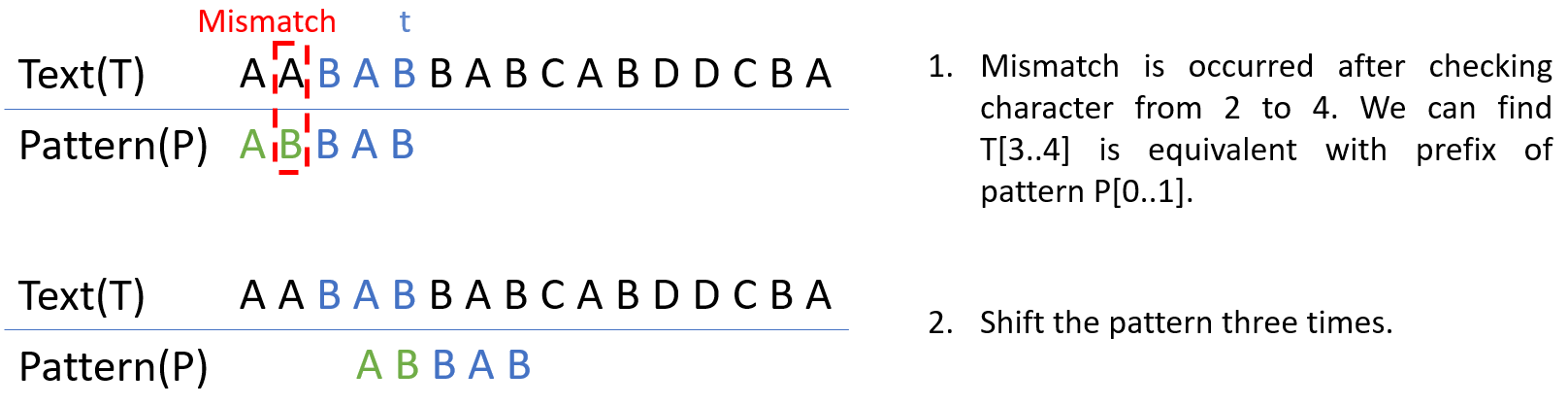
good_suffix_case_2 Good suffix rule case 2 example

Case 3. 위의 두 경우를 제외한 경우

Case 3는 match되었던 string t에 대해서 위의 Case 1, Case 2가 해당되지 않는 경우이다. 이 때는, Pattern의 앞 부분을 확인할 필요가 없기 때문에 Pattern을 길이만큼 shift시킨다.

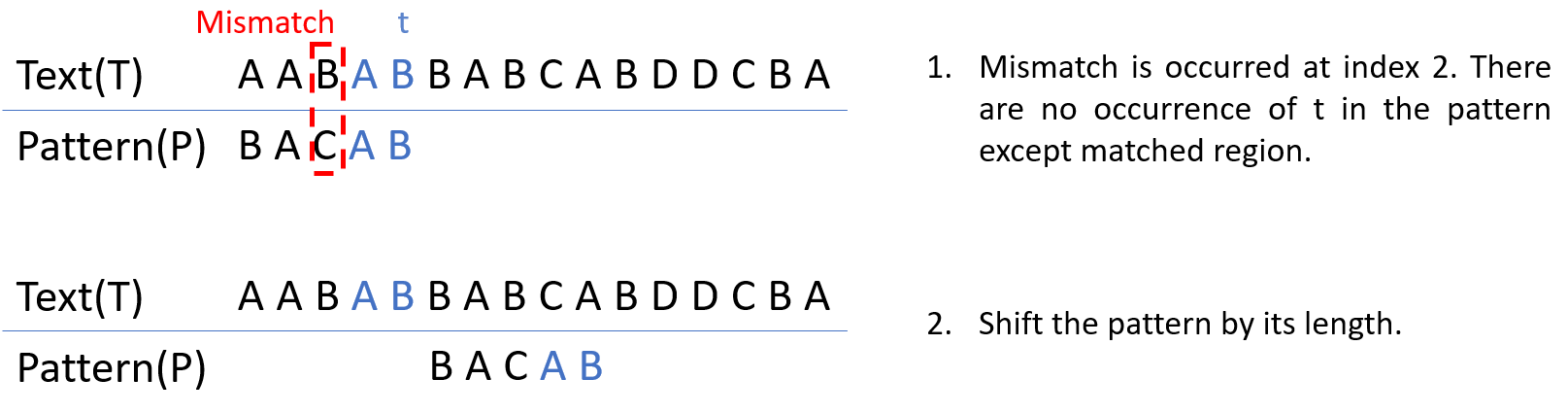
good_suffix_case_3 Good suffix rule case 3 example

※ Strong good suffix rule

이 방식은 앞에서 말한 Case 1과 거의 흡사하다. 하지만, 차이점은 P 내에 t와 일치하는 string이 있다면 바로 이동시키는 것이 아니라 일치하는 string 바로 앞의 문자까지 확인함으로써 불필요한 확인을 막아준다. 다시 말해서, t와 동일한 string 앞의 문자가 mismatch가 일어난 문자와 같은 경우를 무시함으로써 효율을 높이는 것이다.

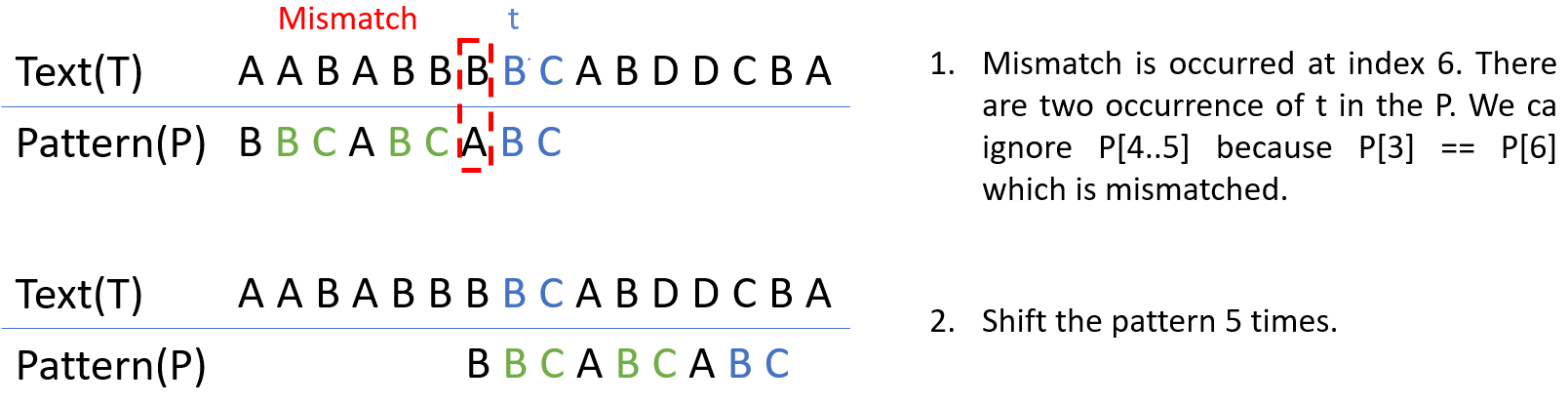
good_suffix_case_0_strong Strong good suffix rule example

구현

1. Preprocess for strong good suffix rule

Good suffix rule을 적용하기 위해서는 먼저 border라는 개념을 알 필요가 있다. Border는 테두리라는 말처럼 string을 감싸는 역활이라고 볼 수 있다. 이를 좀 더 있어 보이게 말하면 suffix와 prefix가 동시에 될 수 있는 string을 의미한다. 예를 들어서 “AATAA”라는 string을 생각해보자. 여기서 “A”와 “AA”모두 prefix와 suffix로 사용될 수 있다. 즉, “AATAA”의 border는 “A”와 “AA”가 된다. 계산시에는 상대적으로 길이가 더 긴 border를 사용한다.

전처리과정에서는 Border의 시작 index를 알려주는 array가 계산된다. Array의 이름을 편의상 bpos라고 하겠다. bpos[i]에는 i번째 index부터 시작하는 sub-string 또는 suffix의 border의 시작 index이 저장된다. 여기서 border의 시작 index는 suffix의 index로 한다. string 위에서 언급한 “AATAA”의 bpos[i]를 계산해보자.

  • bpos[0] : “AATAA”의 border는 “AA”이므로 bpos[0] = 3
  • bpos[1] : “ATAA”의 border는 “A”이므로 bpos[1] = 4
  • bpos[2] : “TAA”의 border는 ““이므로 bpos[2] = 5
  • bpos[3] : “AA”의 border는 “A”이므로 bpos[3] = 4
  • bpos[4] : “A”의 border는 ““이므로 bpos[4] = 5
  • bpos[5] : border가 존재하지 않으므로 bpos[5] = 6

여기서 주목할 점은 bpos[2], bpos[4]와 bpos[5] 이다. 전자의 두 값은bpos가 5로 되어있는데 이는 border가 해당 string에서 존재하지 않기 때문이며 후자는 값을 6(string의 길이 + 1)으로 설정해줌으로써 border가 존재하지 않는 경우에 대한 계산을 쉽게 만들어준다. 다음의 코드는 위에서 언급한 내용들을 언급한 구현 코드이다.

void preprocess_strong_suffix(int *shift, int *bpos,
                  char *pat, int m){
    int i = m, j = m+1;
    bpos[i] = j;
    while(i > 0){
        while(j <= m && pat[i-1] != pat[j-1]) { 
            // 반복해서 shift를 계산하는 것을 방지
            if (shift[j] == 0)
                shift[j] = j-i;
            j = bpos[j];
        }
        i--; j--;
        bpos[i] = j; 
    }
}

여기서 주요 아이디어는 string의 뒤에서부터 시작해서 차례대로 bpos[i]를 구한다는 것이다. 이렇게 했을 때의 장점은 이전에 구한 bpos[i]를 재사용하여 효율을 높일 수 있다는 점이다. 이를 위의 “AABAA”에 대한 예제를 이용해서 다시 살펴보자.

함수에서는 가장 먼저 bpos[5] = 6, bpos[4] = 5가 저장될 것이다. 이후에는, pat[3] == pat[4]이므로 bpos[3] = 4가 된다. 이를 다시 생각해보면 새로운 char와 이전 border 앞의 char가 같으면 이전에 구한 border가 연장되는 것으로 생각해볼 수 있다. 어차피 border가 나타내는 string은 prefix와 suffix의 공통 string이 담겨있기 때문에 새로운 char만 검사하면 되는 것이다.

이 다음에는 pat[2] != pat[3]이므로 기존의 border가 연장될 수 없다. 이는 pat[4]에서 mismatch가 일어나며 pat[3]로 이동하면 된다는 것을 알려주기에 shift array에 저장하며 반복해서 pat[2]와 일치하는 border 앞 character를 확인한다. 이 과정을 반복해서 일치하는 char를 찾을 수 없다면 끝까지 진행되어 bpos[2] = 5가 된다. bpos를 구하는 과정은 위의 두 경우에 대한 계산을 반복하면서 얻어진다.

shift[j] == 0에 대해서만 계산을 진행하는 이유는 동일한 index에 대해서 shift값이 여러 번 계산되어 누락되는 경우를 방지하기 위함이다.

2. Preprocess for case 2

Case 2의 구현은 이전에 구한 Strong good suffix rule보다 훨씬 간단하다. Case 2를 다시 생각해보면 Prefix와 일치하는 이미 검사한 substring t의 Suffix starting index로 이동하는 것으로 생각할 수 있다. Prefix와 일치해야 하기 때문에 계산은 bpos[0]에서부터 시작한다. 만약, 현재 index가 bpos[0]와 같거나 큰 경우네는 bpos[bpos[0]]을 이용하면 더 길이가 짧지만 prefix와 일치하는 suffix에 대한 index를 바로 가져올 수 있다. 이를 적용하는 코드는 다음과 같다.

void preprocess_case2(int *shift, int *bpos, 
                      char *pat, int m) { 
    int i, j; 
    j = bpos[0]; 
    for(i=0; i<=m; i++) { 
        // 이미 shift가 구해져있다면 덮어쓰지 않기 위해서
        if(shift[i]==0) 
            shift[i] = j; 
  
        // bpos[]는 shift를 계산하는 현재 index보다 뒤에 있어야하므로 같아지면 다음 bpos로 이동한다
        // (prefix와 일치함을 유지하면서) 
        if (i==j) 
            j = bpos[j]; 
    } 
}

전체 코드

void search(char *text, char *pat) { 
    // s is shift of the pattern with respect to text 
    int s=0, j; 
    int m = strlen(pat); 
    int n = strlen(text); 
  
    int bpos[m+1], shift[m+1]; 
  
    //initialize all occurence of shift to 0 
    for(int i=0;i<m+1;i++) shift[i]=0; 
  
    //do preprocessing 
    preprocess_strong_suffix(shift, bpos, pat, m); 
    preprocess_case2(shift, bpos, pat, m); 
  
    while(s <= n-m) { 
  
        j = m-1; 
  
        // 현재의 비교 위치(s + j)에서부터 Text와 pattern을 비교
        while(j >= 0 && pat[j] == text[s+j]) 
            j--; 
  
        // j가 0보다 작게되면 pattern과 일치하는 string을 찾은 것
        if (j<0) { 
            printf("pattern occurs at shift = %d\n", s); 
            s += shift[0]; 
        } 
        else
            // 일치하지 않는 경우에는 shift 배열을 이용하여 다음 비교 위치로 이동
            s += shift[j+1]; 
    } 
  
}

마무리

Boyer-Moore algorithm에는 위에서 본 것 처럼 bad character rule과 good suffix rule 두가지의 rule이 존재한다. 어느 하나의 rule을 선택해서 algorithm을 구현하는 것이 아니라 두 방법 모두를 사용하여 shift array를 얻은 후, 비교 불일치가 일어날 때마다 값이 큰 shift array를 이용하면 최적의 Boyer-Moore algorithm을 구현할 수 있게 된다.

Reference

  1. https://www.geeksforgeeks.org/boyer-moore-algorithm-good-suffix-heuristic/
  2. https://en.wikipedia.org/wiki/Boyer%E2%80%93Moore_string-search_algorithm